
Can you give examples of proofs without words? In particular, can you give examples of proofs without words for non-trivial results?
(One could ask if this is of interest to mathematicians [1], and I would say yes, in so far as the kind of little gems that usually fall under the title of 'proofs without words' is quite capable of providing the aesthetic rush we all so professionally appreciate. That is why we will sometimes stubbornly stare at one of these mathematical autostereograms [2] with determination until we joyously see it.)
(I'll provide an answer as an example of what I have in mind in a second)
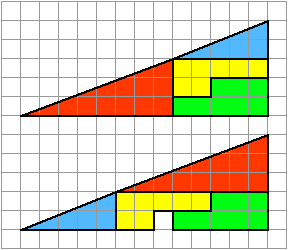
A proof of the identity $$1+2+\cdots + (n-1) = \binom{n}{2}$$
(Adapted from an entry I saw at Wolfram Demonstrations [1], see also the original faster animation [2])
This proof was discovered by Loren Larson, professor emeritus at St. Olaf College. He included it along with a number of other, more standard, proofs, in "A Discrete Look at 1+2+...+n," published in 1985 in The College Mathematics Journal (vol. 16, no. 5, pp. 369-382, DOI: 10.1080/07468342.1985.11972910 [3], JSTOR [4]).
[1] http://demonstrations.wolfram.com/Because I think proof by picture is potentially dangerous, I'll present a link to the standard proof that 32.5 = 31.5:
An animation of the above is:
(This work has been released into the public domain by its author, Trekky0623 at English Wikipedia. This applies worldwide.)
There does not seem to be any necessity for the particular 'path in the relevant configuration space' that was used by the author of the above animated gif. This may be seen as an argument against including an animation.
32.5 = 31.5) is in fact true? - Honest Abe
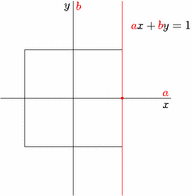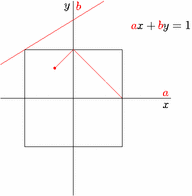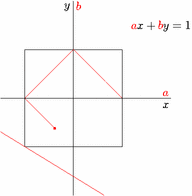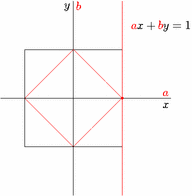
The cardinality of the real number line is the same as that of a finite open interval of the real number line.
It is known (see this other answer [1]) that an 8x8 board in which squares at opposite corners have been removed cannot be tiled with dominoes, as the removed squares are of the same "colour". But what if two squares of different colours are removed? Ralph E. Gomory showed that it is always possible, no matter where the two removed squares are, and this is his proof:
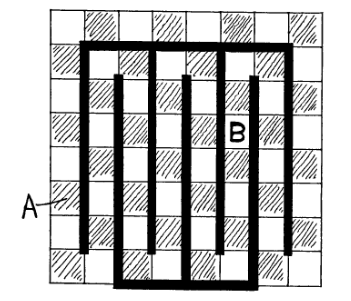
(Imagine A and B are the squares removed.) The image is from Mathematical Gems I by Ross Honsberger.
[1] https://mathoverflow.net/a/9381There are a couple of Fibonacci identities, I think. For example
$F_0^2+F_1^2+\cdots+F_n^2=F_{n}F_{n+1}$, with $F_0=1$.
By putting together squares of side $F_n$, one at a time, you get a rectangle of dimension $F_nF_{n+1}$: The two squares of side 1, then the square of side 2, then the square of side 3 and so on.
Here is an image I found online
This is elementary as well, but one of my favorite ones :)
$1^2 + 2^2 + \dots + n^2 = \frac13n(n+1)(n+\frac12)$
(Author: Man-Keung Siu)
It's a long list of wonderful answers already, but I can't resist...
Question: Is it possible to find six points on a square lattice that form the vertices of a regular hexagon?
Proof without words:
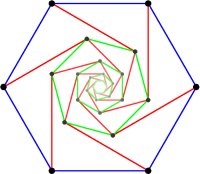
Hint: A square lattice is invariant under rotation by π/2 around any lattice point. Use reductio ad absurdum.
Credit: I learned that proof from György Elekes during the Conjecture and Proof course in the Budapest Semesters in Mathematics, after constructing a proof of my own that used entirely too many words and made very laboured use of the fact that $\sqrt{3}$ is irrational. The picture here is my own creation (using Asymptote).
Follow-up: Can you find four points on a hexagonal lattice that form the vertices of a square? The proof is similar but not immediate.

This visual proof of $$\sum\limits_{n=1}^\infty \left (\frac{1}{2}\right)^{\,2n}=\frac{1}{3}$$ is from http://www.cecm.sfu.ca/~loki/Papers/Numbers/ (Visible Structures in Number Theory, by Peter Borwein and Loki Jorgenson, The American Mathematical Monthly, vol. 108, no. 5, 2002, pp. 897-910).
This might be trivial but integration by parts has a nice proof without words:
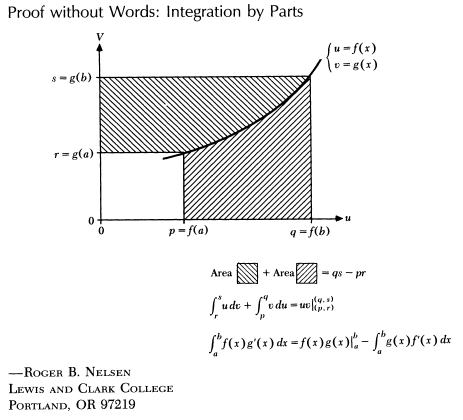
(Got from: Roger B. Nelsen, Proof without Words: Integration by Parts, Mathematics Magazine, Vol. 64, No. 2 (Apr., 1991), p. 130; the original link is https://www.maa.org/sites/default/files/Roger_B04151._Nelsen.pdf).
There's a picture proof in the Princeton Companion, or alternatively on p. 340 of Hatcher [1], of the fact that the higher homotopy groups are abelian. Actually, here's a screenshot of the one in Hatcher (hopefully fair-use!):

Here $f$ and $g$ are mappings (with basepoint) of $S^n$ into some space for $n > 1$; the picture shows a homotopy between $f + g$ and $g + f$.
The above diagrams show an application of the interchange law, a more general expression of the Eckmann-Hilton argument, for double categories or groupoids. Here is a more general picture
which shows that the interchange law for a double groupoid implies the second rule $v^{-1}uv= u^{\delta v} $, where in the picture $a=\delta v$, for the crossed module associated to a double groupoid, taken from the book advertised here [2]. There are many $2$-dimensional rewriting arguments which are essential to the results of this book.
[1] http://pi.math.cornell.edu/%7Ehatcher/AT/AT.pdf
$ $ $ $ $ $ $ $
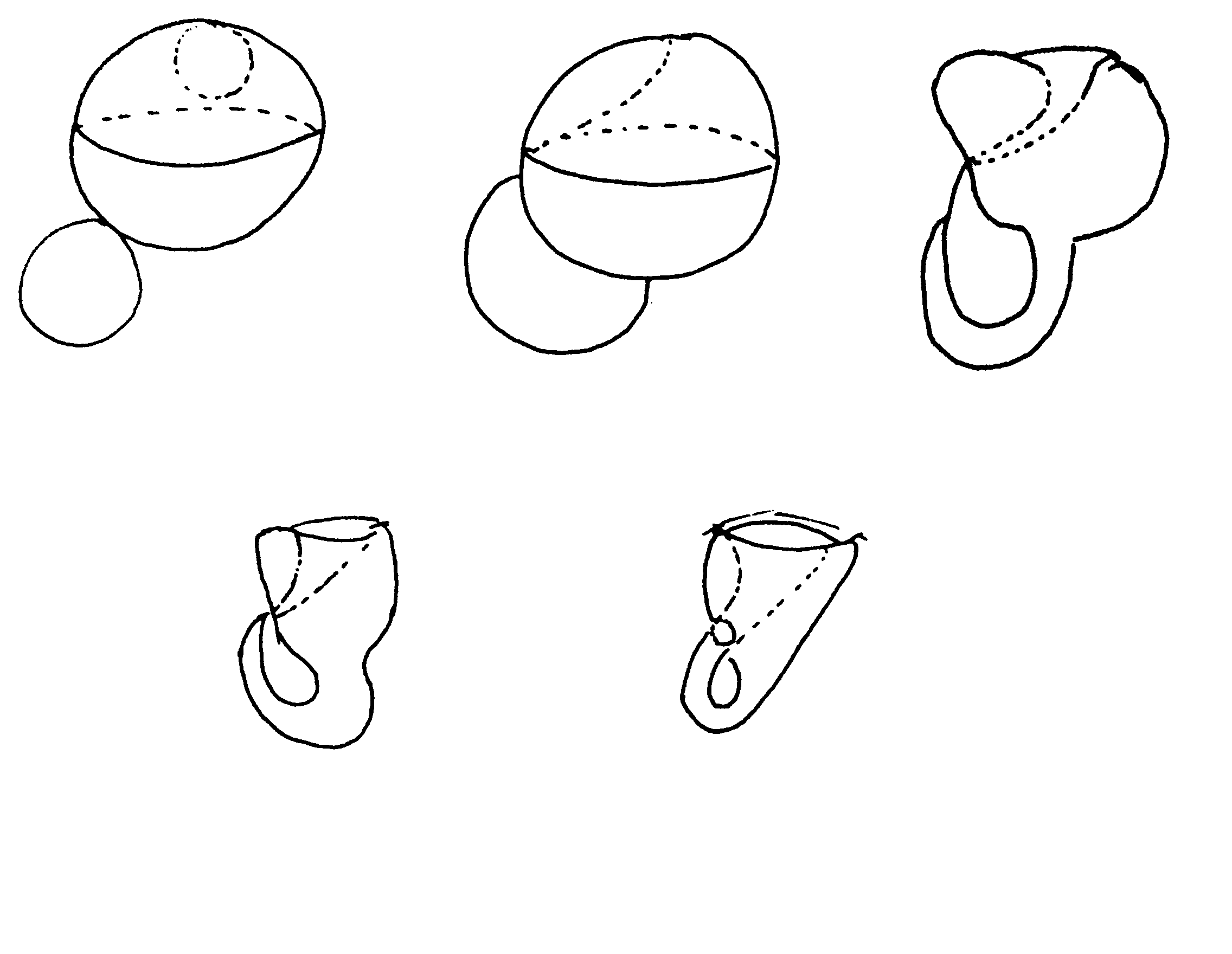
I'm partial to the proof using Dandelin spheres that (certain) cross sections of cones are ellipses, where an ellipse is defined as the locus of points whose total distance to two foci is constant. It's particularly nice because it explains the foci geometrically, as well as the focus-directrix property with some more work.
Means inequalities:
The image was sent to me by James M. Lawrence, grazie! See also page 53 of "Proofs without words: exercises in visual thinking, Volume 2" for a very different layout of the same 4 inequalities.
Another one exists involving the sum $$1^3 + 2^3 + \cdots + n^3:$$
The second image is due to Brian Sears [1] ( Wayback Machine [2])
[1] http://users.tru.eastlink.ca/%7Ebrsears/math/oldprob.htm#s32Another proof of the sum of the first $n$ squares, relying on the knowledge of the formula for the sum of the first $n$ numbers:
$$1^2 + 2^2 + \dots + n^2 = n(n+1)(2n+1)/6$$
This one has a similar flavor to the fabled proof by Gauss of the sum of the first $n$ numbers. It's a good follow up for students after Gauss's proof.
Wikipedia has a few nice proofs of the pythagorean theorem. Elementary, but elegant.

Duality between $\ell^1$ and $\ell^\infty$ norms.
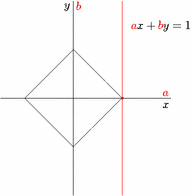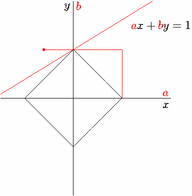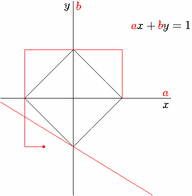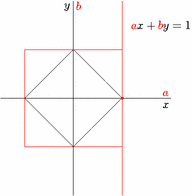
and the reverse animation
If we have 3 circles on the plane with tangent lines, we can notice they have collinear intersection!
To prove it, we can visualize the same configuration in 3D, the balls lay on a surface and rather than tangent lines we take cones: The colinearity comes from the fact that if we lay a plane ontop of this configuration it will intersect the table in a line!
This is from 'curious and interesting geometry' and the proof is attributed to John Edson Sweet. I really like this proof because it gives a vivid example of the general idea that sometimes, to solve a problem in the most simple way you need to view it as a part of some bigger whole.
I'm quite surprised no-one pointed out this one yet:
Theorem. The trefoil knot is knotted.
Proof.
Some comments: a 3-colouring of a knot diagram D is a choice of one of three colours for each arc D, such that at each crossing one sees either all three colours or one single colour. Every diagram admits at least three colourings, i.e. the constant ones. We'll call nontrivial every 3-colouring in which at least two colours (and therefore all three) actually show up. It's easy to see (one theorem, more pictures!) that Reidemeister moves preserve the property of having a nontrivial 3-colouring, and that the unknot doesn't have any nontrivial colouring.
The picture shows a (nontrivial) 3-colouring of the trefoil.
EDIT: I've made explicit what "nontrivial" meant ― see comments below. Since I'm here, let me also point out that the number of 3-colourings is independent of the diagram, and is itself a knot invariant. It also happens to be a power of 3, and is related to the fundamental group of the knot complement (see Justin Robert's Knot knotes [2] if you're interested).
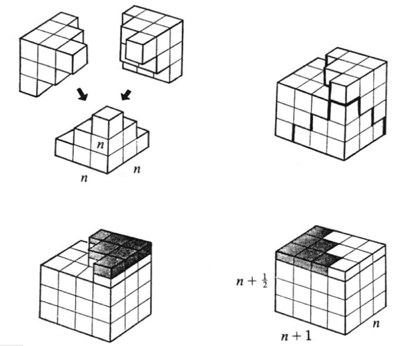
[1] http://poisson.phc.unipi.it/~golla/trefoil.pngHere's a proof of the inequality of the arithmetic and geometric means in the form $$\frac{x_1^n}{n} + \cdots + \frac{x_n^n}{n} \geq x_1\cdots x_n.$$
Proof for $n=3$:
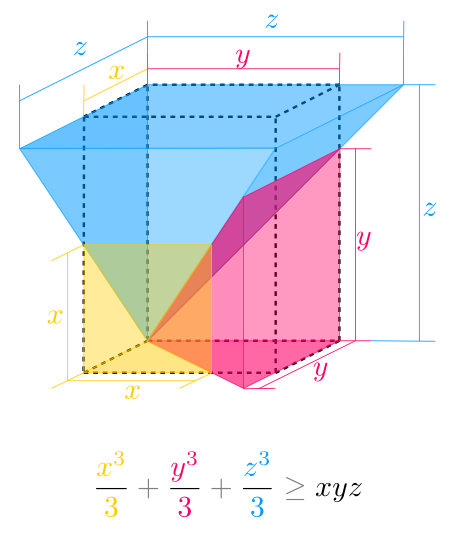
The "figure" for general $n$ is similar, with $n$ right pyramids, one with an $(n-1)$-cube of side length $x_k$ as its base and height $x_k$ for each $k=1,\ldots,n$.
(I made this in Inkscape [1], a wonderful free-software vector drawing application. For the inequality and associated labels, I used the textext [2] extension.)
[1] http://www.inkscape.org/from Steven Strogatz's column: http://opinionator.blogs.nytimes.com/2010/04/04/take-it-to-the-limit/ ( Wayback Machine [1])
[1] http://web.archive.org/web/20201109032840/https://opinionator.blogs.nytimes.com/2010/04/04/take-it-to-the-limit/Here is the very first piece of original mathematics I ever did, in high school:
The derivative of sine is cosine.

The sequence of pictures
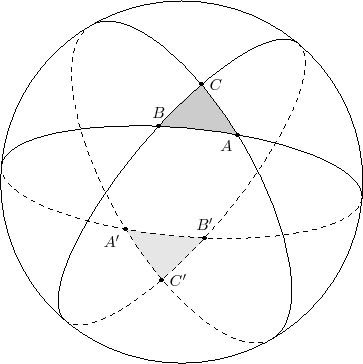
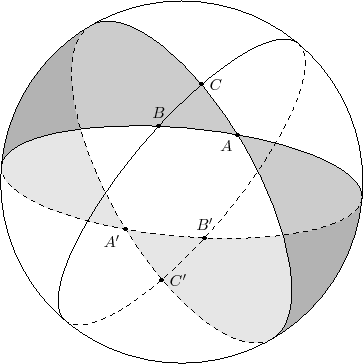
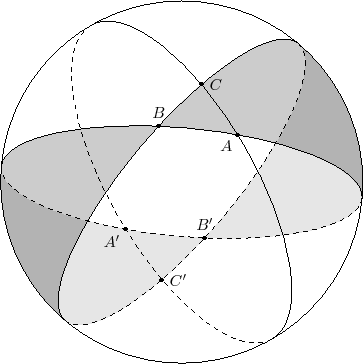
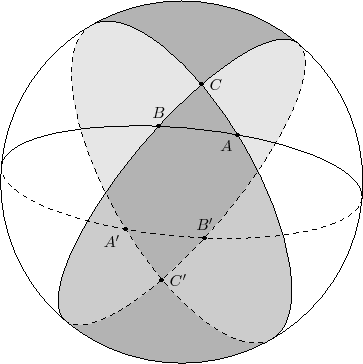
proves the area formula for spherical triangles ${\rm area}(ABC)=\hat{ABC}+\hat{BCA}+\hat{CAB}-\pi$.
Late to the party, but David Lehavi and Bob Palais both mentioned the proof that $\pi_1(SO(3))$ has an element of order 2. In fact it is the only nontrivial element, and so the double cover of $SO(3)$ is simply connected.
Here's an animated illustration of that fact, courtesy of Wikipedia ( here [1]):

Algebraic manipulations in monoidal categories can also be performed in a graphical calculus. And the best part is that this is completely rigorous: a statement holds in the graphical language if and only if it holds (in the algebraic formulation). See for example Peter Selinger's " A survey of graphical languages for monoidal categories [1]". There are many instances, for example in knot theory studied via braided categories. The following specific example comes from Joachim Kock's book " Frobenius Algebras and 2D Topological Quantum Field Theories" [2], and proves that the comultiplication of a Frobenius algebra is cocommutative if and only if the multiplication is commutative.

$$\arctan \frac{1}{3} + \arctan \frac{1}{2} = \arctan 1$$
It's easy to generalize this to
$$ \arctan \frac{1}{n} + \arctan \frac{n-1}{n+1} = \arctan 1, \text{ for } n \in \mathbb{N}$$
which can further be generalized to
$$ \arctan \frac{a}{b} + \arctan \frac{b-a}{b+a} = \arctan 1, \text{ for } a,b \in \mathbb{N}, a \leq b $$
Edit: A similar result relating Fibonacci numbers to arctangents can be found here [1] and here [2].
[1] http://www.futilitycloset.com/2016/06/05/a-guest-appearance/Sphere eversion [1]
This proof-without-words of the Pythagorean Theorem is far from a new one, but it's the first one I've ever seen 'in the wild' (this photo was snapped after finishing dinner at a Mongolian Grill restaurant):
A classic one, from the late 19th century, that surprized Peano's contemporaries.
Question : "A curve that fills a plane ? You must be kidding"
Answer :
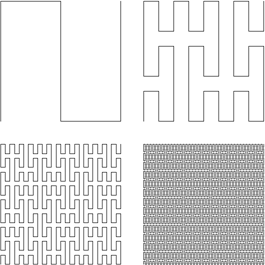
Well, of course a formal proof was necessary, but it is still one of my favorites.
I wonder why Apostol's proof of the irrationality of $\sqrt{2}$ [1] - which is as visual as a proof can be (in my opinion) - has not been mentioned: One can literally see at a glance that it proves what it's supposed to prove: the impossibility of a isosceles right triangle with integer side length (by infinite descent):
Note that it's not a proof completely without words. It helps a lot to read the comments of the author:
Each line segment in the diagram has integer length, and the three segments with double tick marks have equal lengths. (Two of them are tangents to the circle from the same point.) Therefore the smaller isosceles right triangle with hypotenuse on the horizontal base also has integer sides.
But through own thinking one could come up with this by oneself (having in mind what's to be proved).
[1] http://hipatia.dma.ulpgc.es/profesores/personal/aph/ficheros/resolver/ficheros/crp/2root_2000.pdfI am surprised that no one had cited the "proof" that the rationals are countable yet. See, for example, this picture

As you probably already know — there are lots of these in Proofs without Words [1] (and II) by Roger Nelson.
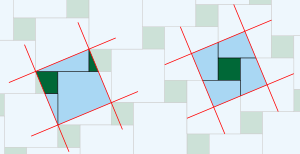
[1] https://rads.stackoverflow.com/amzn/click/com/0883857006The cover of Peter Winkler's first book is a great proof without words of a statement which I'll leave you to guess, regarding the combinatorics of tiling a hexagon with rhombi.
EDIT: I think the guessing game isn't helpful. The statement is that when tiling a perfect hexagon with the appropriate kind of rhombi of various orientations, the number of tiles in each orientation is the same. The image is slightly misleading in its use of color; there ought to be just three colors, corresponding to the three orientations.

Conway and Soifer tried to set a record for least number of words in a mathematical paper. I've reproduced it here in its entirety.
Can n2 + 1 unit equilateral triangles cover an equilateral triangle of side > n, say n + ε?
John H. Conway & Alexander Soifer
Princeton University, Mathematics
Fine Hall, Princeton, NJ 08544, USA
conway@math.princeton.edu asoifer@princeton.edu
n2 + 2 can:
(I'd post this as a comment to Mariano Suárez-Alvarez, but I've not enough rep). From a ME thread [1].
$$\sum_{k=1}^n (-1)^{n-k} k^2 = {n+1 \choose 2} = \sum_{k=1}^n \; k = \frac{(n+1) \; n}{2}$$
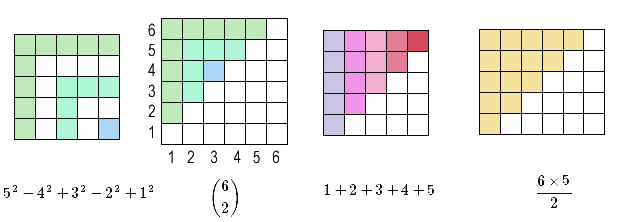
I just saw this proof, which is of course not mine.
Proof with words: The [area of a] circle [1]
Similar in concept to the above video:
[1] https://youtu.be/whYqhpc6S6gIn an attempt to push the bar towards the non-trivial, I'll mention the proof that the boundary complex of every polytope is shellable. The proof is virtually word-free but requires an actual movie rather than a still image: imagine yourself in a spaceship, taking off in a straight line from one of the facets, away from the polytope. Every once in a while a new facet is visible to you; under assumptions of general position, this provides a shelling of the complex (obviously, you need to fly off to projective infinity and come back on the other side).
This was assumed by Euler but first proved only in 1970 by Brugesser and Mani, who said that the idea came to him in a dream. More details here [1] (search for "shellability") or here [2].
[1] https://gilkalai.wordpress.com/2009/01/16/telling-a-simple-polytope-from-its-graph/A line that bisects the right angle in a right triangle also bisects a square erected on the hypotenuse:
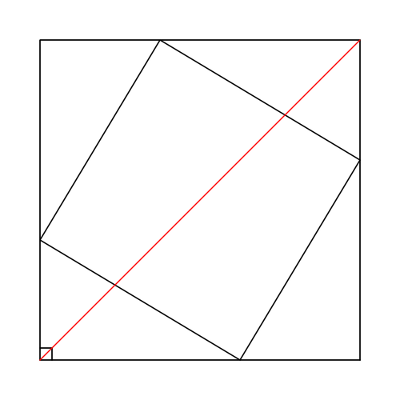
source: https://www.futilitycloset.com/2011/09/12/half-and-half/
This should really be a comment on Marco Radeschi's answer [1] from Feb 22 involving the area formula for spherical triangles, but since I'm new here I don't have the reputation to leave comments yet.
In reply to Igor's comment (on Marco's answer) wondering about an analogous proof for the area formula of hyperbolic triangles: there is one along similar lines, and you're rescued from non-compactness by the fact that asymptotic triangles have finite area. In particular, the proof in the spherical case relies on the fact that the area of a double wedge with angle $\alpha$ is proportional to $\alpha$; in the hyperbolic case, you need to replace the double wedge with a doubly asymptotic triangle (one vertex in the hyperbolic plane and two vertices on the ideal boundary) and show that if the angle at the finite vertex is $\alpha$, then the area is proportional to $\pi - \alpha$. That follows from similar arguments to those in the spherical case (show that the area function depends affinely on $\alpha$ and use what you know about the cases $\alpha=0,\pi$).
Once you have that, then everything follows from the picture below, since you know the area of the triply asymptotic triangle and of the three (yellow, red, blue) doubly asymptotic triangles.
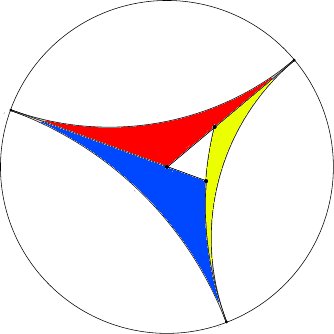
(That picture is slightly modified from p. 221 of this book [2], which has the whole proof in more detail.)
[1] https://mathoverflow.net/questions/8846/proofs-without-words/16064#16064The area under a cycloid is three times the area of the generating circle.

$ $ $ $
[1] http://www.cl.cam.ac.uk/~mj201/images/mutilated-chess-board2.gifIn the movie category, I'm surprised that no-one has yet posted a link to Moebius Transformations Revealed [1].
[1] https://www.youtube.com/watch?v=JX3VmDgiFnYFrom the book "Proofs without words", there are ton of others too but this one I had trouble proving in UG, so like it most.
Given three mutually tangent circles in the plane, there exist exactly two circles tangent to all three.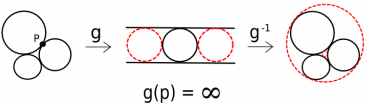
Have a look at this document from an MIT-instructor (Sanjoy Mahajan): http://mit.edu/18.098/book/extract2009-01-21.pdf
(This is a draft of Chapter 4 of: Sanjoy Mahajan, Street-Fighting Mathematics , MIT Press 2010 [1].)
[1] https://mitpress.mit.edu/books/street-fighting-mathematicsGluing two Mobius strips along their edges is a Klein bottle. [1]
[1] https://www.youtube.com/watch?v=a5Azcwe9p4oThe pathspace of any topological space is contractible.
Pf (as given in my homotopy theory class): slurp spaghetti.
The first homotopy group of SO_3 has an order 2 element (that's a classic).
The surface area of a quarter of the unit sphere is Pi via Gauss-Bonnet (My source is Ariel Shaqed - it should have been a classic, but no one I asked seems to knew it). The sphere is what you reach with a straight hand while standing still. Hold a Pencil in your hand, that's your tangent vector. Now parallel transport the pencil on a quarter sphere: it points in the opposite direction. QED
Proof of the associativity law $f * (g * h) = (f * g) * h$ in the fundamental groupoid of a topological space:
You can find more of these diagrams in J. P. May's A Concise course in algebraic topology.
I like the tiling proof of the Pythagorean Theorem. The left image is credited to Al-Nayrizi and Thābit ibn Qurra (9th century) and the right by Henry Perigal (19th century).
This is an example I did when I was in high school.
Let it be a unit disc, consider the length of horizontal line, we know:
$\text{Yellow}=2\cos \frac{3}{7}\pi$, $\text{Yellow}+\text{Green}=-2\cos \frac{5}{7}\pi$, $\text{Red}+\text{Green}=2\cos \frac{1}{7}\pi$.
Then
$1=\text{Red}=\text{Red}+\text{Green}-(\text{Green}+\text{Yellow})+\text{Yellow}= 2(\cos \frac{3}{7}\pi+\cos \frac{5}{7}\pi+\cos \frac{1}{7}\pi).$
Also elementary, but here is a proof that
$C_n = \binom{2n}{n} - \binom{2n}{n+1} = \frac{\binom{2n}{n}}{n+1},$
where $C_n$ is the $n$th Catalan number.
http://utdallas.edu/~hagge/images/Catalan.pdf [1] ( Wayback Machine [2])
Sorry for the link; new users may not use image tags.
Here's the image:
$S^2 \vee S^1 \vee S^1$ is homotopy equivalent to the Klein bottle with self-intersection.
Posted this quite a while ago on math.SE as an answer to https://math.stackexchange.com/q/733754/214353; I think it has a place here too.
To be rigorous, it maybe only proves that $f(z):=\displaystyle\lim_{n\to\infty}\left(1+\frac zn\right)^n$ is $1$ at integer multiples of $2\pi i$ (perhaps also that $f$ is $2\pi i$-periodic), but does not give any insight into why $f(z)=\text{something}^z$; still...
I've seen it much better rendered once somewhere on the web but could not find it again, so tried to reconstruct it myself
I was somehow challenged by the idea: do more abstract topics allow proofs without words? I came out with this example. Of course, it is disputable if it is really "without words", since some words of explanation should be given (here they are: vertical segments represent Banach spaces and subspaces; connecting segments between two of them represent a linear operator. Italic letters $a,b,c,d,e$ are the dimensions of the corresponding linear subspaces).
Here [1] you can find Grace Lin's proof without Words that The Product of the Perimeter of a Triangle and Its Inradius Is Twice the Area of the Triangle (see the figure below)
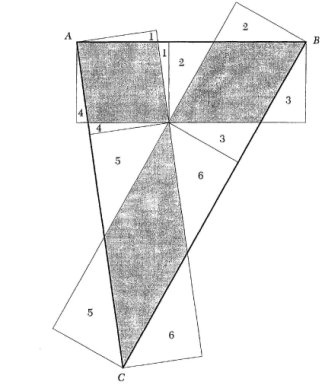
The proof originally appeared in the 1999 October issue of Mathematics Magazine.
[1] http://www.maa.org/sites/default/files/269122948517.pdfI've tried to read carefully through all the posts here, and I think no one has mentioned the excellent book by R.B. Nelsen which contains many more such examples. I give here an explicit citation:
Nelsen, Roger B. Proofs without words: Exercises in visual thinking. No. 1. MAA, 1993.
Here is an example which I have recently used:

A crucial step in proving the triangle inequality for the $L^p$ norms is to prove Young's inequality: $ab \leq \frac{a^p}p + \frac{b^q}q$ when $a,b>0$ and $p,q > 1$ are conjugate ($\frac 1p + \frac 1q=1$). This can be proved by comparing the areas in the following picture:
An easy calculus exercise gives the blue area as $\frac{a^p}p$ and the green area as $\frac{b^q}q$, hence their sum dominates the area $ab$ of the rectangle outlined in red.
I learned this proof from Cohn's measure theory book, where it appears as an exercise (in Section 3.3).
The idea is to prove things in ways that are obvious to different parts of your brain, right? Anyone found any "auditory proofs"? Some candidates -
Nyquist sampling theorem?
sin[a] + sin[b] = 2sin[(a+b)/2]cos[(a-b)/2]. If you use at and bt instead of a and b, you can translate that to show how the addition of two sine tones close in frequency can also be perceived as a modulation or "vibrato" around the centre frequency. The factor of 2 might be hard, though you can add a gain instead of 2 and show that the difference is silence when the gain is 2 :)
Sampling in frequency domain (comb filter) is periodicity in time domain?
Here are some "audio illusions" though, for your amusement - http://www.youtube.com/watch?v=e6JSTkwXg90
Can you tile an 8x8 chessboard with one corner cut off with dominoes of dimension 3x1?

This is a simple way to show that choosing a useful coloring can make a proof trivial.
This proof was also a result of the Conjecture and Proof class in the Budapest Semesters in Mathematics. It was one of the first problems encountered there, hence not that hard :)
There is a proof of Erdös-Mordell Inequality [1] 'without words' which an impressive one. Please follow the link http://forumgeom.fau.edu/FG2007volume7/FG200711.pdf
[1] https://en.wikipedia.org/wiki/Erd%C5%91s%E2%80%93Mordell_inequalityLet $0\leq x,y,z,t\leq1$ Prove that $x(1-y)+t(1-x)+z(1-t)+y(1-z)\leq 2$.
Draw a 1x1 square and mark in consecutive sides disjoint segments starting at the vertexes of lengths $x,y,z,t$. Joining the consecutive end points of the intervals that are not vertexes of the square form four triangles, the area of the triangles is the left hand side divided by 2, the area of the square is the right hand side divided by 2.
There is a beautiful proof of the fact that a checkerboard with sides $2^{n}$, and one square removed can be tiled with $L$-shaped pieces formed by three squares. Given that a checkerboard of sides $2^{n-1}$ can be so tiled, then a square checkerboard of sides $2^{n}$ can be tiled by filling in the quarter in which the removed piece lies, and then placing an extra $L$-shaped tile with one square in each of the remaining three quarters.
Proof of the lantern relation (taken from the book: A Primer on Mapping Class Groups by Farb, B. and Margalit, D.)
This image is a bijection between the puzzle rule and the semistandard tableau rule for Littlewood-Richardson coefficients. It is taken from this paper of Ravi Vakil [1], where it is attributed to Terry Tao.
The picture generalises to a bijection between rules in K-theoretic Schubert calculus, but I haven't seen a picture and don't currently have the patience to create one.

I just scanned some old drawings, and found this one that fits right in.
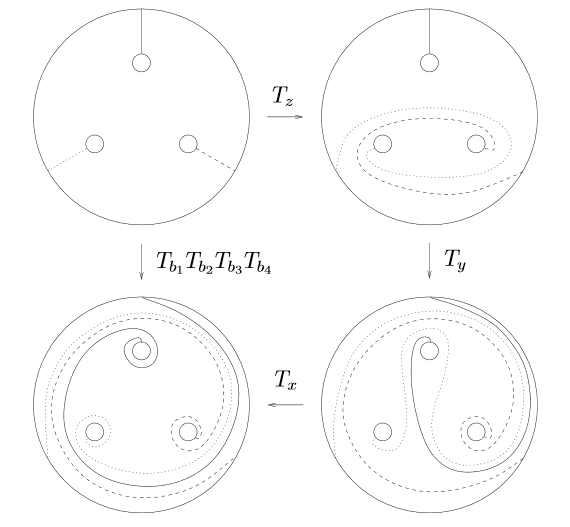
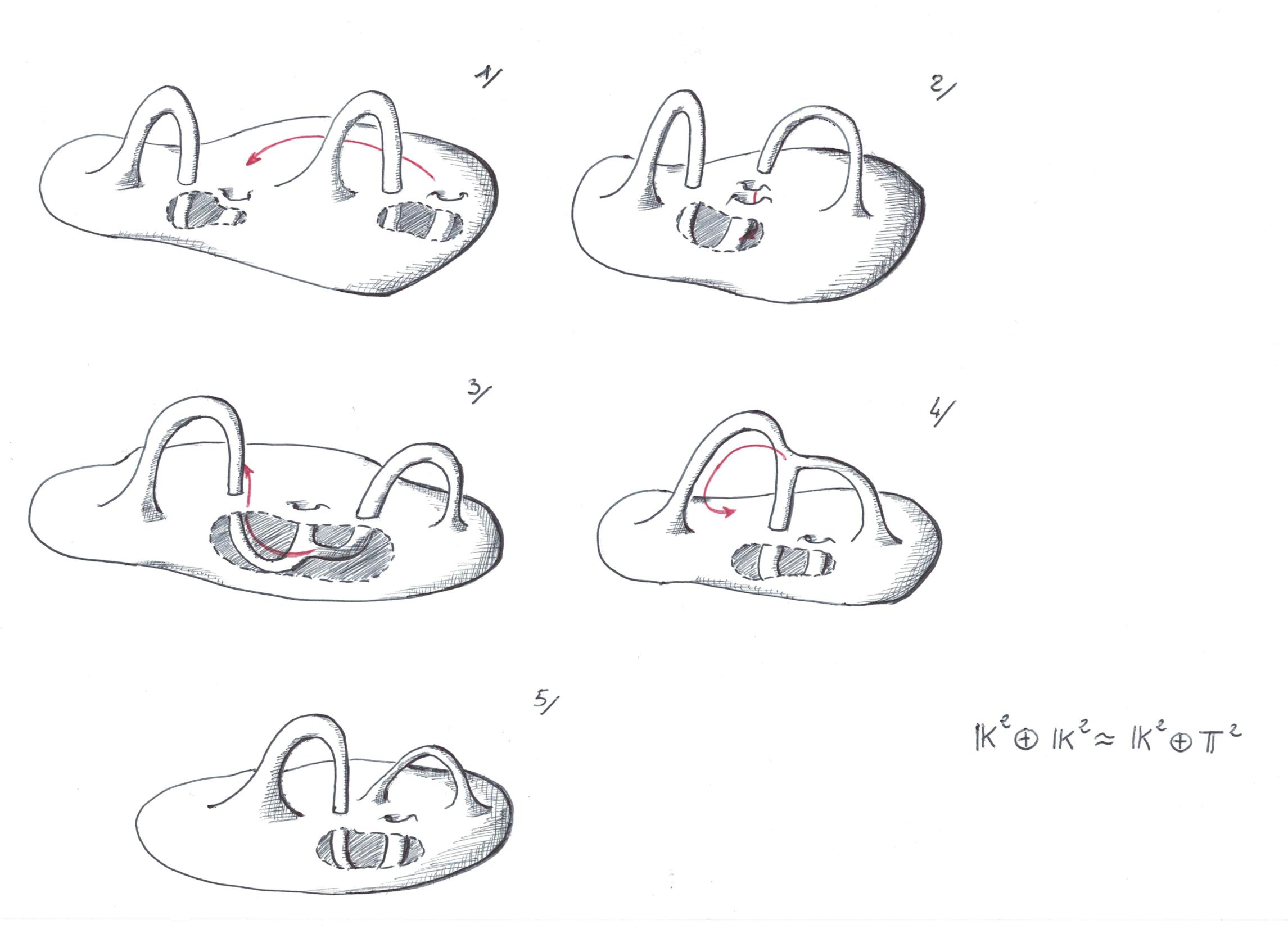
It proves that the connected sum of two Klein bottles is homeomorphic to the connected sum of a Klein bottle and a Torus.
This is apparently not was intended, but I think it qualifies. From Principia Mathematica [1]: the proof of 1+1=2 [2].
[1] https://en.wikipedia.org/wiki/Principia_MathematicaThere are $\binom{n+2}{4}$ equilateral triangles in the regular $n$-vertices-per-side triangular grid, by choosing $A<B<C<D$ from the set $\{1,...,n+2\}$: https://arxiv.org/abs/2211.00186
Rich Schwartz had on his site a great paper consisting of only a picture which proved that every right triangle admits a periodic billiard path. Unfortunately, he's since deleted it, so I can't post it here. (It shouldn't take too long for anyone interested to re-construct the proof, though.)
Interesting how everyone understands "proof without words" as "proof made of pictures". I read the title and immediately thought that every proof can be written without words, using just first order logic. I stopped there and thought that this is just another language, using different words - and I came to the conclusion that there can not be a mathematical proof without "words", because you have to get some information across! Sure, you can use different languages than English. But in the end, this boils down to the question, what is a word?
BTW: Unmentioned so far are category-theoretical proofs, which can sometimes be expressed very comprehensively as a sequence of diagrams. I am too lazy to look up a good example, because I already explained that I don't believe in the question.
A 3D proof of a Fibonacci identity, that even includes a video:
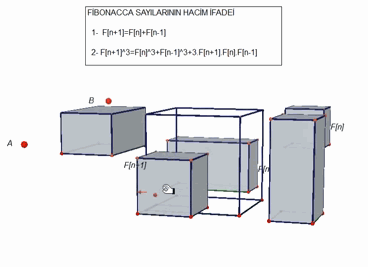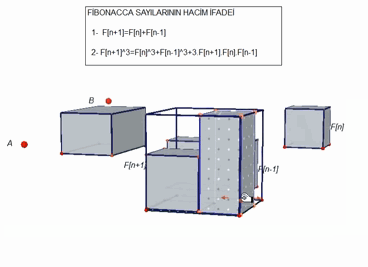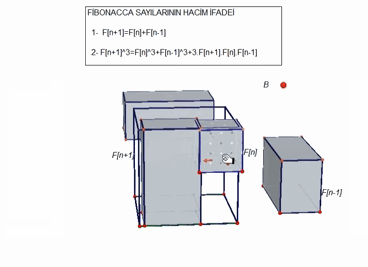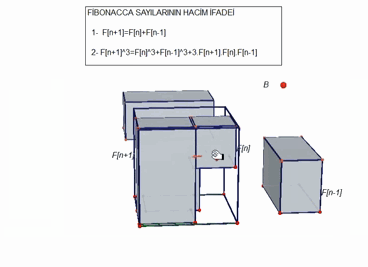
The picture below proves (without words) that it is possible to draw the classical Desargues configuration [1] $D_{10}$ using points in the set $\{-3,-2,-1,0,1,2,3\}^2$. This picture was produced by Alex Ravsky as the answer to this MO-question [2].
[1] https://en.wikipedia.org/wiki/Desargues_configurationTrig angle-sum and angle-difference formulas, by Blue on Math SE [1]


Here are some dynamic versions:
http://www.math.utah.edu/~palais/sums.html (two of the summation formulas mentioned above)
Several belt, plate, and tangle trick animations:
http://www.math.utah.edu/~palais/links.html
A visual derivation of complex multiplication:
http://www.math.utah.edu/~palais/newrot.swf
Pythagoras in the Isosceles case, based on the Yale tablet:
http://www.math.utah.edu/~palais/PythagorasIsosceles.html
and the general case:
http://www.math.utah.edu/~palais/Pythagoras.html
I suggest the videos of Viennot explaining the bijections between different families of objects counted by Catalan numbers:
http://www.xavierviennot.org/contscience/videos.html
Here's a proof of the area of a circle (or sector) which is different from the one posted previously.
EDIT: I was unable to embed the file, which is in pdf form. Here is a link:
http://wildpositron.files.wordpress.com/2011/04/sectorarea2.pdf
I discussed what goes into making the proof complete to show that the map preserves area on my blog here (it requires just another picture or two, but it's essentially still only a geometric argument):
http://wildpositron.wordpress.com/2011/04/05/calculating-the-area-of-a-sector/
This is not entirely without words, but Byrne's edition of Euclid's elements has cut down the number of words to a bare minimum.
http://www.math.ubc.ca/~cass/Euclid/byrne.html
More visual proofs of Nicomachus's Identity [1]

Mediawiki user Cmglee. (Maybe it is already in Nelson's book - I don't have it)
[1] https://en.wikipedia.org/wiki/Squared_triangular_numberFrom Wikipedia: here is a "proof without words" of the Yoneda Lemma.

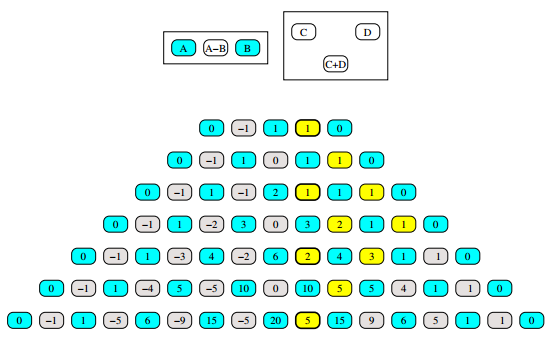
For $0 \lt k \lt n$,
$$\binom{n}{k} = \frac{n}{n-k}\binom{n-1}{k}$$
How k-subsets of [n], marked dark green in the rows, come from k-subsets of [n-1] after n-fold duplication and rearrangement:
 Exactly $n-k$ times:
Exactly $n-k$ times:
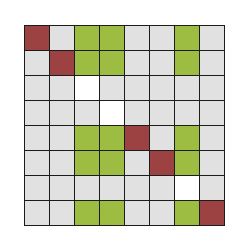
By induction, a base case, and taking $k=n$ and $k=0$ for granted: $$\binom{n}{k} = \frac{n}{(n-k)} \frac{(n-1)!}{(n-1-k)!\ k!} = \frac{n!}{(n-k)!\ k!}$$
Michael Goldberg, Constructions possible by ruler and compasses [1], Math. Mag. Vol. 51, No. 5, p. 283 (1 page) (Nov., 1978).
[1] https://doi.org/10.2307/2690247
The composition of two continuous mappings is continuous.
This is a "proof without words" by an equation, not a picture.
Three complex numbers $a,b,c$ in the complex plane form the vertices of an equilateral triangle if and only if $~a^2 + b^2 + c^2 = ab + bc + ca$:
$$ $$
$$ \hspace{-3in} 2 |a^2 + b^2 + c^2 - ab - bc - ca|^2 $$ $$ = ( |a-b|^2 - |b-c|^2)^2 + ( |b-c|^2 - |c-a|^2)^2 + ( |c-a|^2 - |a-b|^2)^2 . $$